
# 목적
캘리포니아 인구조사 데이터를 사용해 캘리포니아 주택 가격 모델 만들기.
학습시킨 모델에 다른 측정 데이터가 주어졌을 때 구역의 중간 주택 가격을 예측해야 함.
# 파라미터 설명
- total_rooms: 전체 방의 개수
- total_bedrooms : 전체 침실 개수
- population : 인구 수
- households : 세대 수
- median_income : 중간 소득
- median_house_value : 중간 주택 가격
- ocean_proximity : 바다 근접도
- longitude : 경도
- latitude : 위도
- housing_median_age : 주택 지어진 기간(중앙값)
1단계 : 문제 정의
이번 작업은 "지도 학습" or "비지도 학습" or "강화 학습" or etc... 중에 무엇일지 정해야 한다.
정답은 "지도 학습" 이다. 현재 나는 레이블된 훈련 샘플이 있기 때문이다. 그리고 가격을 예측해야 하므로 '회귀'를 사용하여야 한다.
회귀분석에는 두 가지 종류가 있다.
- 단변량 회귀 : 하나의 특성을 기반으로 예측
- 다변량 회귀 : 여러개의 특성을 기반으로 예측
이번 경우는 구역의 인구, 중간 소득 등 feature 가 많으므로 다변량 회귀의 경우이다.
2단계 : 성능 측정 지표 선택
회귀 분석의 대표적인 성능 측적 지표는 평균 제곱근 오차(RMSE; Root Mean Square Error) 이다.

** RMSE 공식 설명 **
n = 데이터셋에 있는 샘플의 수
x^(i) = i 번째 샘플의 전체 특성값의 벡터
y^(i) = i 번째 샘플의 기대 출력값
h : 예측 함수이자 가설(hypothesis)
시스템이 하나의 샘플 데이터 x^(i)를 받으면 예측 함수에 대입되어 예측 값이 출력된다. RMSE가 회귀 문제에서 주로 선호되는 성능 측정 지표이지만 경우에 따라 이상치가 많은 구역이 있다면 평균 절대 오차(Mean Absolute Error)를 고려할 수 있습니다.

3단계 : 데이터 가져오기
데이터를 가져오는 코드는 제외했다.
housing.head()
간략히 housing의 데이터를 보았다.
특성은 10개이다.
housing.info()
-------------------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 20640 non-null float64
1 latitude 20640 non-null float64
2 housing_median_age 20640 non-null float64
3 total_rooms 20640 non-null float64
4 total_bedrooms 20433 non-null float64
5 population 20640 non-null float64
6 households 20640 non-null float64
7 median_income 20640 non-null float64
8 median_house_value 20640 non-null float64
9 ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB무언가가 보인다. total_bedrooms.....
여기에서 얻어야 할 정보
1. ocean_proximity 속성만 object 형이고 나머지는 숫자이다.
2. total_bedrooms 에 207개가 특성을 가지고 있지 않다. (나중에 해결해야 할 듯 하다.)
housing["ocean_proximity"].value_counts()
-------------------------------------------
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64ocean_proximity 속성의 value 값을 확인했다.
housing.describe()
숫자형 특성들의 요약 정보를 확인하였다.
# 히스토그램 - 데이터 형태를 빠르게 파악하기
%matplotlib inline
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show()
여기에서 주의해야 할 사항은 다음과 같다.
- 중간 소득(median_income)이 달러 단위가 아니다.
- 중간 주택 연도(housing median age) 와 중간 주택 가격(median house value) 의 오른쪽 그래프가 심하게 높아진 것을 볼 수 있다. 아마 마지막 값으로 한정시킨 것으로 생각하면 된다. 중간 주택 가격의 특성은 예측하는데 레이블로 사용되기 때문에 아마 오른쪽 심하게 높아진 데이터를 어떻게든 처리해야 할 것 같다.
# 데이터 나누기
train_set, test_set = train_test_split(housing, test_size = 0.2, random_state = 123)
print(len(train_set), "train +", len(test_set), "test")
-----------------------------------------------------------------------------
16512 train + 4128 test사이킷런에서 지원하는 train_test_split() 을 이용하여 train 80%, test 20% 로 데이터를 나누었다.
데이터를 나누면서 알아야 할 것은 샘플링 편향이다.
데이터가 충분히 많다면 상관 안해도 되지만 적다면 샘플링 편향이 생길 가능성이 있다. 우리는 무수히 많은 데이터에서 대표할 수 있는 데이터를 뽑아야 하고, 이를 계층적 샘플링(stratified sampling) 이라고 부릅니다.
지금 경우에서는 중간 소득이 중간 주택 가격을 예측하는 데 매우 중요한 지표라고 가정한다면, 테스트 세트(test set)는 전체 데이터셋에 있는 여러 소득 카테고리를 잘 대표해야 합니다. 중간 소득은 숫자형이므로 소득에 대한 카테고리를 만드는 것이 의미가 있을 것입니다.
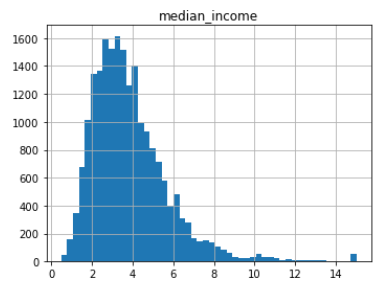
중간 소득의 분포를 살펴보면 $20,000 ~ $50,000 사이에 주로 많은 데이터를 가지고 있지만 $60000 이상의 데이터도 있기도 합니다. 계층별로 데이터셋은 충분히 있어야 합니다. 그렇지 않으면 계층의 중요도를 판단할 때 편향이 생길 수 있습니다.
housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
housing["income_cat"].where(housing["income_cat"] < 5, 5.0, inplace=True)
housing["income_cat"].hist()
plt.show()housing 에 "income_cat" 이라는 새로운 column을 만들어냈습니다.

소득에 대한 카테고리를 만들고 히스토그램을 구성하였습니다.
카테고리 수를 제한하기 위해 1.5 를 나누었고, ceil() 함수를 이용해 올림을 진행했습니다. 5보다 크다면 전부 5로 가는 걸로 설정하였습니다.
# 계층 샘플링하기
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=123)
for train_index, test_index in split.split(housing, housing["income_cat"]):
imsi_train_set = housing.loc[train_index]
imsi_test_set = housing.loc[test_index]imsi_test_set["income_cat"].value_counts() / len(imsi_test_set)
-----------------------------------------------------------------
3.0 0.350533
2.0 0.318798
4.0 0.176357
5.0 0.114583
1.0 0.039729
Name: income_cat, dtype: float64# 전체 주택 데이터셋에서의 소득 카테고리 비율
housing["income_cat"].value_counts() / len(housing)
----------------------------------------------------
3.0 0.350581
2.0 0.318847
4.0 0.176308
5.0 0.114438
1.0 0.039826
Name: income_cat, dtype: float64
# 카테고리 형성을 위해 만들었던 income_cat 삭제하기
for _ in (imsi_train_set, imsi_test_set):
_.drop("income_cat", axis=1, inplace=True)4단계 : 데이터 시각화
housing = imsi_train_set.copy()전체 데이터를 이해하는데 훈련 세트만 보고 탐색하기 위해 복사하였다. 훈련 세트가 크면 별도로 샘플링해야 할 수 있지만 지금 경우는 큰 경우가 아니니 그대로 간다.
# 지리적 데이터 시각화
ax = housing.plot(kind="scatter", x="longitude", y="latitude", alpha = 0.1)
ax.set(xlabel='경도', ylabel='위도')

alpha 값을 주면 밀집도를 더욱 정확하게 확인할 수 있다.
# 주택 가격 적용
ax = housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="인구", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
ax.set(xlabel='경도', ylabel='위도')
plt.legend()
plt.show()
원의 반지름은 인구를 나타내고, 색깔은 가격을 나타냅니다. 자세히 보면 바다 근처가 집 가격이 더 크다는 것을 알아낼 수 있습니다. 물론 바다 근처인데도 불구하고 가격이 높지 않은 지역이 있어 이러한 정보를 사용할 때 간단하지는 않을 것 같습니다.
# 상관관계 조사
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)
-------------------------------------------------------
median_house_value 1.000000
median_income 0.687160
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population -0.026920
longitude -0.047432
latitude -0.142724
Name: median_house_value, dtype: float64상관관계를 보면 중간 주택 가격(median_house_value)은 중간 소득(median_income)과 양의 상관관계를 가지며 중간 소득이 올라 갈 때 증가한다. 위도(latitude)와는 음의 상관관계로 위도가 올라갈 수록 가격이 서서히 내려간다고 볼 수 있다. 0에 가까운 것은 관계가 없다는 뜻.
상관계수는 선형적인 관계만 측정 가능하다. 비선형은 측정 불가.
상관계수는 기울기와 관계가 없다.
# 중간 주택 가격과 중간 소득을 산점도로 나타내기
housing.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.1)
plt.show()
이 산점도를 보고 알 수 있는 것은 갈 수록 증가하는 상향관계를 알 수 있다는 것입니다. 그리고 퍼져있지 않고 몰려있어서 아주 좋은 특성입니다. 하지만 $500,000 에서 제한값으로 수평선으로 보이고, $350,000 과 $280,000, $230,000 등 수평선이 보입니다. 이러한 데이터는 좋지 않으므로 삭제하는 것이 좋습니다.
# Feature 조합해보기
머신러닝 알고리즘용 데이터를 준비하기 전에 또 한가지 해보면 좋을 것이 특성 조합이다.
housing["rooms_per_household"] = housing["total_rooms"] / housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"] / housing["total_rooms"]
housing["population_per_household"]=housing["population"] / housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
---------------------------------------------------------------------------------
median_house_value 1.000000
median_income 0.687160
rooms_per_household 0.146285
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population_per_household -0.021985
population -0.026920
longitude -0.047432
latitude -0.142724
bedrooms_per_room -0.259984
Name: median_house_value, dtype: float64특성을 조합하여 새로운 조합 3가지를 나누어보았다. 그 중 rooms_per_household 가 각각의 total_rooms와 households보다 상관관계가 높게 나타났다. 이런 feature 가 좋다는 것은 아니지만 이러한 방법도 있다는 것이다.
다음 게시물은 드디어 머신러닝을 돌리기 위한 데이터를 준비할 단계이다.
To be continue....
'개인 프로젝트' 카테고리의 다른 글
| 캘리포니아 주택 가격 예측 모델 만들기 - (2) feat.특성 스케일링 (0) | 2020.09.17 |
|---|