Jerry StoryWalk

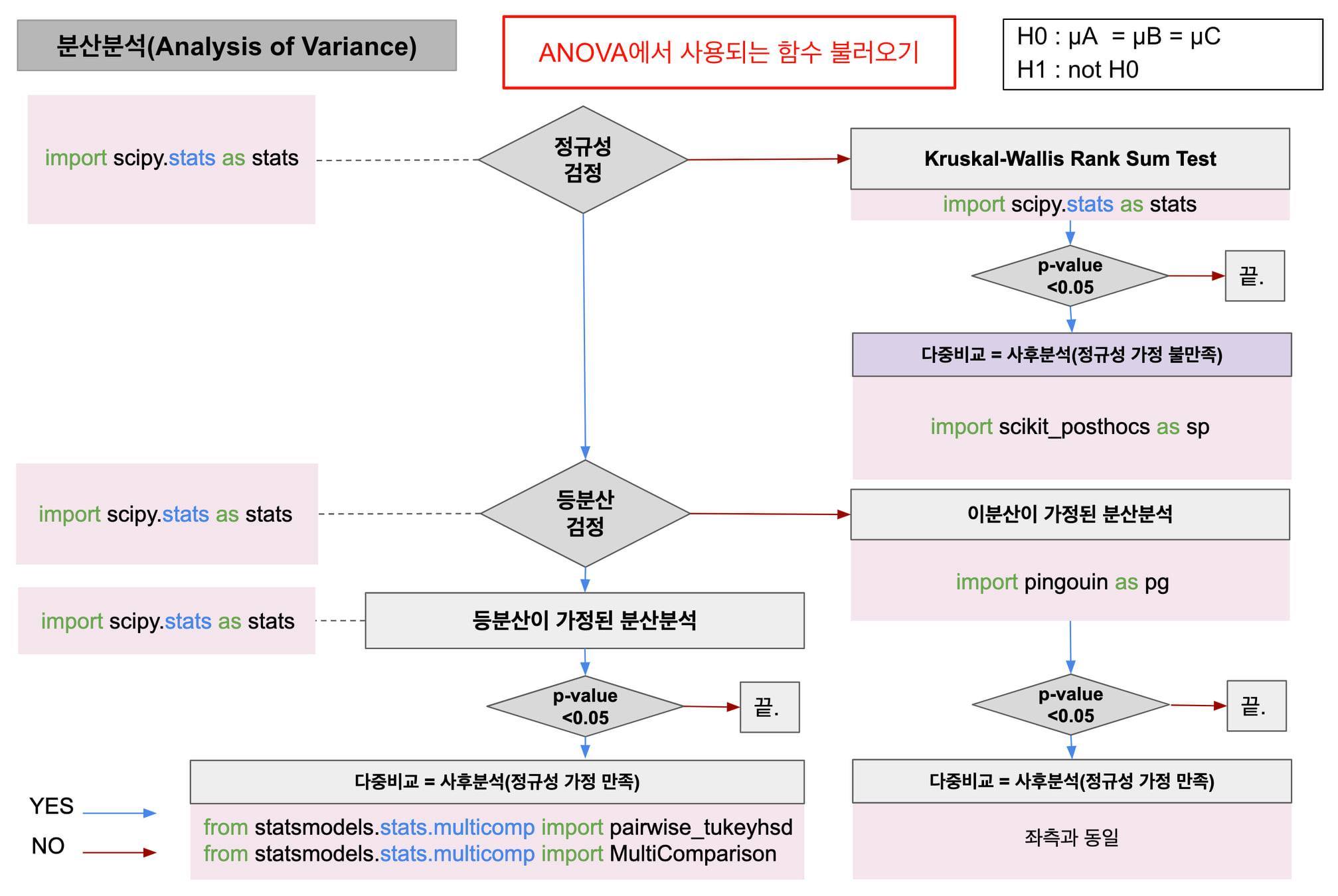
이전 게시물에 이어서 이번에는 상관 분석을 파이썬을 통해 알아보자. 귀무가설 : 꽃잎의 길이와 꽃받침의 길이 간에는 관련성(직선의 관계)이 없다.대립가설 : 꽃잎의 길이와 꽃받침의 길이 간에는 관련성(직선의 관계)이 있다. 1. Pearson stats.pearsonr(x = iris.petal_length, y = iris.sepal_length)---------------------------------------------------------------(0.8717537758865832, 1.0386674194497525e-47) Person 방법은 stats.pearsonr() 을 사용한다. 0.872 : 표본의 상관계수(r)0.000 : 유의확률 유의확률이 0.000 이므로 유의수준 0.05에..

상관분석(Correlation Analysis) 상관분석은 쉽게 말하면 직선(선형)의 관계가 있는지 분석하는 것이다.상관분석에서 알아야 할 점은 [산점도], [상관계수] 이다. 상관 분석의 핵심은 Y를 예측하는 것이고 X 들에 대해 얼마나 선형 관계가 강하고 약한지 파악한다. (featuring) 예를 들어 X_1의 자료가 질적자료이고 A와 B가 있을 때는 Two sample test를 진행하여 Y와의 관계를 파악해 볼 수 있고, A,B,C,D, 등의 질적자료가 있을 때는 분산분석(ANOVA)를 이용할 수도 있을 것이다. X와 Y라는 양적자료가 있을 때 대부분 더 중요한 양적 자료를 Y로 둔다. 분산분석에는 "일원배치 분산분석" 이라는 것이 있다. 질적인 자료 하나를 가지고 양적인 자료와 차이가 있는지 ..

이전 게시물에 이어서 만약 등분산이었을 때의 분산분석을 해보자. stats.f_oneway(iris.loc[iris.species == "setosa", "petal_length"], iris.loc[iris.species == "versicolor", "petal_length"], iris.loc[iris.species == "virginica", "petal_length"]) ------------------------------------------------------------------------- F_onewayResult(statistic=1180.161182252981, pvalue=2.8567766109615584e-91) 등분산 일 때의 분산분석은 stats.f_oneway() 를 사..

분산 분석(ANOVA : Analysis of Variance) k 개의 집단을 비교하여 다름을 판단하는 것. (k : 3개 이상의 유한한 개수) 분산 분석의 대립가설은 많은 경우의 수를 가지고 있다. 그래서 최소한 2개의 집단은 차이가 있을 것으로 판단한다. 일표본 검정 -> 독립 2표본 -> 분산분석 -> 회귀분석으로 확장된다. 모집단 A, B, C 가 있고 모두 정규분포를 따른다고 가정한다. 각각의 모집단에서 표본을 추출하는데 데이터 2개씩 가져온다고 가정해보자. 우리는 뽑아낸 표본들의 데이터들에 대해 Y의 다름이 얼마나 되는지 측정하고 싶다. 하지만 데이터에서 전체 평균을 빼고 모두를 더하면 무조건 0 이 나온다. 그래서 그 편차를 제곱을 한다. SST = SSE(Sum of Square Erro..

# 카이제곱 검정(Chi-square : χ2) 질적자료와 질적자료간에 서로 통계적으로 관계가 있는지 판단하는 검정 카이제곱 분포를 기반으로 관찰된 빈도와 기대되는 빈도와 의미있게 다른지 여부를 검증한다. 예시를 통해 알아보자. - 예제 데이터 수집 귀무가설 : 성별과 사람이 안경을 쓰는 것은 관련성이 없다. 대립가설 : 성별과 사람이 안경을 쓰는 것은 관련성이 있다. 만약 합계는 변하지 않는다고 가정했을 때 귀무가설이 맞다면 예상할 수 있는 값이 있을 것이다. 그것이 바로 기대값(Expected Value) 이다. 그래서 관찰된 값과 기대값 사이의 차이가 거의 없으면 귀무가설을 따를 수 있다. 하지만 관찰된 값과 기대값 사이의 차이가 많다면 대립가설을 따를 수 있다. 이 때, 기대값을 모두 더한 값은 ..

♪ 대응 2표본 검정 - (1) Paired t-test - (2) Wilcoxon's signed rank test 이전 게시물에서는 대응 2표본 t 검정(Paired t-test) 에 대해서 알아봤다. 하지만 정규성이 만족했을 때의 이야기이므로 이번에는 정규성 가정이 깨졌을 때를 이야기해보자. Wilcoxon's signed rank test 사전(pre)과 사후(post)가 함께 있으니 두 집단처럼 보이지만 사전 - 사후 이니 결국 한 집단이다. 결국 D(difference) 만 본다면 일표본 검정과 같아진다. 그래서, 사전의 양적 자료와 사후의 양적 자료를 뺀 값이 정규성 가정을 만족하지 않을 때 사용한다. [가설검정] 귀무가설 : 다이어트는 몸무게를 줄이는 것에 효과가 없다. (사전 몸무게 = ..

♪ 대응 2표본 검정 - (1) Paired t-test - (2) Wilcoxon's signed rank test ※ 대응표본(paired sample) - 두 모집단으로부터 표본을 각각 추출할 때 표본 각각의 인자가 서로 대응되는 표본 - 사전(pre)과 사후(post)를 비교할 때 주로 사용한다. 만약에 이런 질문을 받았다고 생각해보자. "다이어트 프로그램이 체중 감량하는데 효과가 있다는 것을 증명해봐!" 이런 상황일 때 대응 2표본 검정을 실행시키면 된다. 모집단 A(Pre) 와 모집단 B(Post)가 있다고 가정하자. 각 모집단에는 인자들이 있을 것이고 서로 대응한다. 예를 들어, 다이어트 프로그램을 하기 전(Pre)과 후(Post) 라고 정하였다. 귀무가설은 "다이어트 프로그램을 하기 전의 ..

♪ 독립 2표본 검정 - 두 개의 독립적인 모집단에 대한 평균에 통계적으로 유의한 차이가 있는지를 검정하는 방법. - 독립 : A 집단의 양적 자료가 B 집단의 양적 자료에게 영향을 주지 않는 상태 이제 과정을 진행해보겠다. 독립 2표본은 모집단이 2개가 존재한다. (모집단 A, 모집단 B) 평균은 모집단을 대표하는 값이다. 귀무가설 : A집단의 평균과 B집단의 평균은 같다. 대립가설 : A집단의 평균과 B집단의 평균은 같지 않다. 유의수준 = 0.05 귀무가설과 대립가설이 주어졌다. 이제 귀무가설과 대립가설 중 하나를 선택하기 위해서는 모집단에서 표본을 추출하여 평균을 알아보자. 가정해 보았을 때 A 표본의 평균 - B 표본의 평균 = 0 이라면 귀무가설에 가까울 것이고, A 표본의 평균 - B 표본의..

일표본 t 검정을 공부하기에 앞서 가설검정에 대해 알아보겠다. ※ 가설검정이란? 모집단에 대한 입장(주장)에 대해 표본을 추출하여 수집된 데이터에 근거하여 그 입장(주장)이 맞다고 할 수 있는지를 통계적으로 검정하는 것이다. 가설에는 "귀무가설" 과 "대립가설" 이 있다. 귀무가설(歸無假說; Null hypothesis) : 모집단에 대한 기존의 생각(입장) 대립가설(對立假說; alternative hypothesis) : 귀무가설과 다른 새로운 생각(입장) 표본의 데이터를 근거로 귀무가설과 대립가설 중에서 하나를 선택하는 과정이 가설검정이다. import scipy.stats as stats # 분석에 필요한 라이브러리 ♪ 일표본 t 검정(One sample t-test) - 한 개의 모집단을 이루고 ..

통계에서 가설의 종류는 귀무가설(Null Hypothesis)이 있고 대립가설(Alternative Hypothesis)이 있다. 귀무가설 영가설(零假說) 이라고도 불리며, 별 차이가 없는 경우의 가설이다. 대립가설 귀무가설과는 다른 가설을 주장한다. p-value(유의확률) 귀무가설을 기각할 수 있는 최소한의 유의 수준이다. 유의 수준 : 귀무가설 또는 대립가설의 기준점 유의 수준 > p-value 이면 대립 가설을 채택 유의 수준 < p-value 이면 귀무 가설을 유지